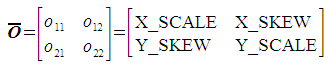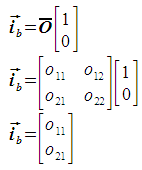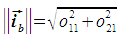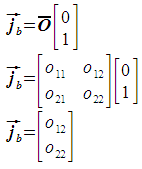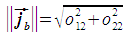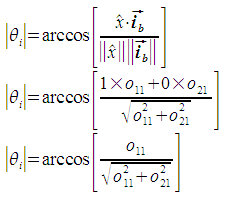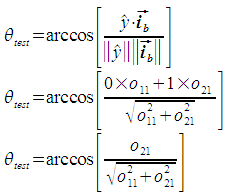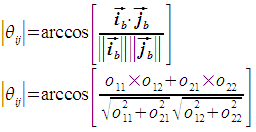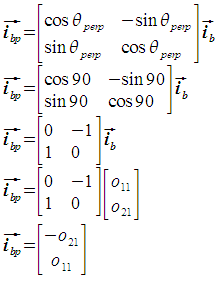How to calculate "real" parameters from affine transformation

Introduction

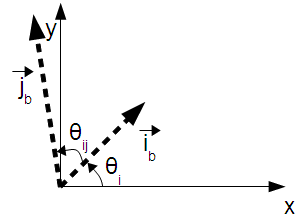
This page discusses how to compute physically significant parameters from an arbitrary linear transformation. The reverse process, calculating the affine parameters from the physically significant parameters, is articulated on another wiki page. The model used to describe how the raster maps onto real world coordinates is illustrated in the following figure:

This model contains all of the parameters except for translation. Translation may be added in after the coordinates have been scaled, rotated and sheared. The above illustration contains the physically significant parameters which will be calculated by this method. These are: θ_i, θ_ij, and the pixel size along the i_b and j_b basis vectors.

The inputs to this method are the four non-translation (non-offset) parameters of a linear transform. These are shown below:

Although these parameters have "common names" within the GIS community, the names are both lengthy and misleading. Within the context of this page, the coefficients o₁₁, o₁₂, o₂₁, and o₂₂ will be used.

This page is divided into sections. Each section describes the computation of one physically significant parameter.

Pixel size in the i direction

To calculate the pixel size in the i direction, the i unit vector is projected using the given transform. This gives the basis vector i_b, the magnitude of which is the pixel size. The basis vector is expressed as follows:

The pixel size is then calculated as follows:

Pixel size in the j direction

The pixel size in the j direction is computed in a manner similar to the pixel size in the i direction. The only difference is that the j unit vector is used in place of the i unit vector. This gives the basis vector j_b, the magnitude of which is the pixel size. The basis vector is expressed as follows:

The pixel size is then calculated as follows:

Rotation

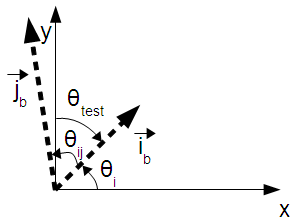
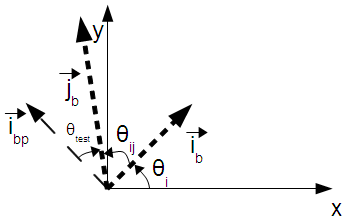
The grid is rotated by the angle θ_i. This is the angle between the x axis of the reference frame and the i_b basis vector. The angle θ_i is considered positive in the clockwise direction, for consistency with compass headings. The calculation of θ_i is a two-step process: first the magnitude is calculated, then the sign is determined. Both steps involve using the ​dot product to determine the angle between θ_i and one of the axes of the target coordinate system (either the x axis or the y axis. The equations in this section refer to the angles and vectors defined in the following figure:

The first step is to calculate the magnitude of the angle between i_b and the x axis. This is the magnitude of θ_i.

The angle θ_i is defined as the angle from the x axis to i_b. It is positive in the clockwise direction. In the situation described in the above figure, this means that θ_i is negative if i_b is above the x axis, and positive if below. We determine whether i_b is above or below the x axis by finding the angle between i_b and the y axis. If i_b and the y axis are separated by less than 90 degrees, i_b is above the x axis, otherwise it is below.

So, if θ_test is less than 90, θ_i = - abs(θ_i). Otherwise, θ_i = abs(θ_i).

Basis vector separation angle

In this section, the method to calculate θ_ij is presented. This is similar to the method for the calculation of θ_i, but it is accomplished with respect to the rotated reference frame of i_b and i_bp instead of the x and y axes. The figure which represents this setup is as follows:

The first step is to calculate the magnitude of θ_ij, the angle between i_b and j_b.

Next, we need to determine the sign of θ_ij in a manner similar to how the sign for θ_i was determined. The angle θ_ij always represents the angle from i_b to j_b, and is positive counterclockwise for consistency with a right-handed coordinate system. To do this, we first need to calculate i_bp, which is perpendicular to i_b and forms a ​right-hand coordinate system with i_b. Observe that i_bp is i_b after a 90 degree counterclockwise rotation.

Now we can determine the size of the angle between j_b and i_bp. In this situation, any angle less than 90 degrees means that j_b is on the same side of i_b as i_bp. An angle more than 90 degrees means it lies on the opposite side.

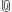
So, if θ_test is more than 90 degrees, θ_ij = - abs(θ_ij). Otherwise, θ_ij = abs(θ_ij).

See also

• Wikipedia article on the ​dot product.
• Wikipedia article on ​coordinate systems.

The forward calculation

On the wiki page describing the reverse operation, a transform is developed which supports:

1. scaling
2. clockwise rotation around the origin
3. shearing parallel to the x axis
4. shearing parallel to the y axis

For the sake of consistency, we will use this same model and attempt to calculate the conceptually meaningful parameters from the transform coefficients. The above model produced the following equations:

• a₁₁ = o₁₁ = s_x ( (1 + k_x k_y) cosθ + k_y sinθ )
• a₁₂ = o₁₂ = s_x ( k_x cosθ + sinθ )
• a₁₃ = t_x
• a₂₁ = o₂₁ = s_y ( -(1 + k_x k_y) sinθ + k_y cosθ )
• a₂₂ = o₂₂ = s_y ( - k_x sinθ + cosθ )
• a₂₃ = t_y

where:

• s_x : scale factor in x direction
• s_y : scale factor in y direction
• t_x : offset in x direction
• t_y : offset in y direction
• θ : angle of rotation clockwise around origin
• k_x : shearing parallel to x axis
• k_y : shearing parallel to y axis

Solving for the meaningful parameters

The objective of this page is to find a way to determine values for s_x, s_y, t_x, t_y, θ, k_x, and k_y if all we know is a₁₁,a₁₂, ... a₂₃. Clearly, t_x and t_y are trivial cases, because we can just use the values for a₁₃ and a₂₃ respectively. This leaves us with these four equations:

• a₁₁ = o₁₁ = s_x ( (1 + k_x k_y) cosθ + k_y sinθ )
• a₁₂ = o₁₂ = s_x ( k_x cosθ + sinθ )
• a₂₁ = o₂₁ = s_y ( -(1 + k_x k_y) sinθ + k_y cosθ )
• a₂₂ = o₂₂ = s_y ( - k_x sinθ + cosθ )

Unfortunately, these four equations contain five unknowns: s_x, s_y, θ, k_x, and k_y. This represents an ill-posed problem and forces us to simplify. Let's assume that there is no shearing. We are just going to declare upfront that k_x=0 and k_y=0. Remember that we did that because if we're wrong it will screw everything up. This makes the above into:

• a₁₁ = o₁₁ = s_x cosθ
• a₁₂ = o₁₂ = s_x sinθ
• a₂₁ = o₂₁ = - s_y sinθ
• a₂₂ = o₂₂ = s_y cosθ

Now we're on a roll. We can knock out s_x and s_y very easily:

• a₁₁² + a₁₂²
  • = s_x² cos²θ + s_x² sin²θ
  • = s_x² (cos²θ + sin²θ)
  • = s_x² (1)
• a₂₁² + a₂₂²
  • = (- s_y)² sin²θ + s_y² cos²θ
  • = s_y² (sin²θ + cos²θ)
  • = s_y² (1)

Rewriting as a "final result", this gives:

• s_x² = a₁₁² + a₁₂²
• s_y² = a₂₁² + a₂₂²

Checking against wikipedia

Checking this against the wikipedia page on the ​world file, which lists:

• "pixel width" = s_x = sqrt(A² + D²) = sqrt(a₁₁² + a₂₁²)
• "pixel height" = s_y = sqrt(B² + E²) = sqrt(a₁₂² + a₂₂²)

Clearly, this does not match the answer on our page. The three possibilities are: we made a mistake; they made a mistake; or no one made a mistake, but we're using different models... The world file page does not declare it's assumptions about what operations are performed, or which order they are performed in. The world file page, however, also defines it's parameter A (for us: a₁₁) as "pixel size in x direction".

NOTE: If the order of the model operations changes, in particular if scaling and rotation are swapped, then these pages match wikipedia. However, the math on wikipedia is unsourced. Since it has become clear that order is vital, and it is by no means guaranteed that all software performs uses the same model, it is probably vital to go out and determine which software performs the calculations which way before we do anything else.