Explanation of distance-calculation, overview

The distance-calculation of today is investigating every combination of vertexes and every combination of vertex against edge between vertexes in the two geometries inputed. If there is many vertexes this procedure is very heavy and slow. I have tried to find a way to narrow the distances calculated. The idea is only applicable on geometries not intersecting. Hopefully there will come up some good idea how to solve that. Until then the easiest is to check for intersecting bounding boxes (of subgeoms) and if thats the case pass it back to the old calculation.

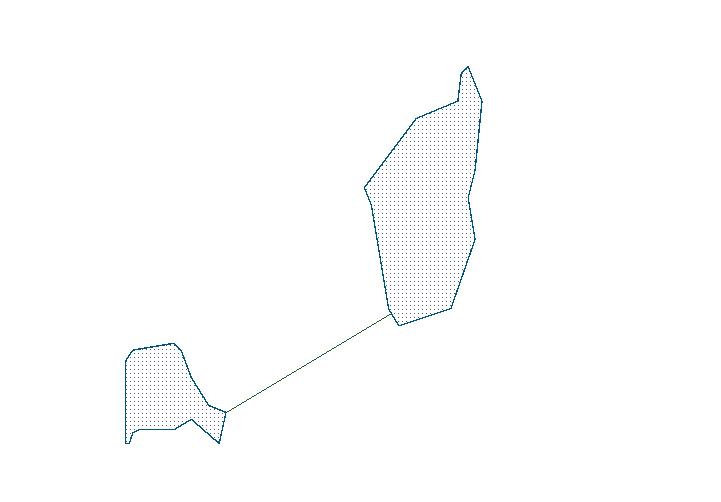
Here I will try to explain the idea in a good way. Here is two polygons that we want to calculate the smallest distance between.

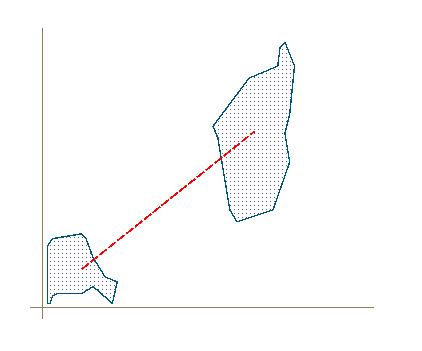
We start by finding an appropriate line between the polygons. The best one is the line between the center of the bounding boxes.

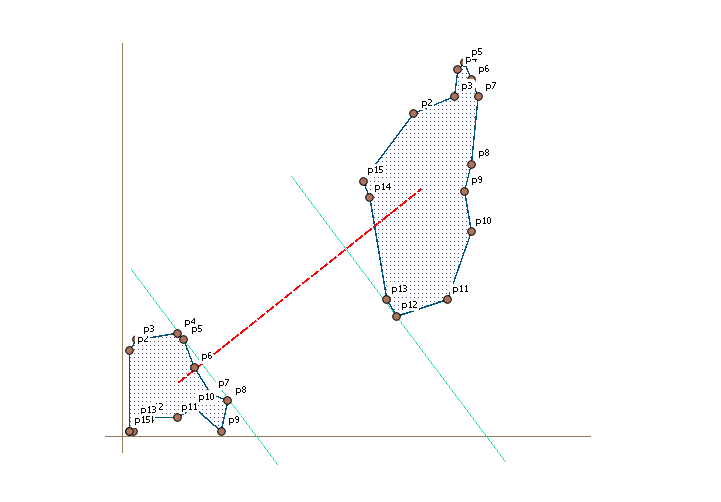
Now we want to find how every vertex is placed along this line. We illustrate this with two perpendicular lines describing p5 in polygon1 and p12 in polygon2.

Where those lines cross the x-axis gives us a value of where the points is situated along the line. We store that value for each vertex and order the vertexes by this value. P5 in polygon1 has the highest value of polygon1 and p12 has the lowest of polygon2. The first distance we calculate is between those two points. Because we not will calculate the points in ring order we have to also check the edge before and after, so we are testing polygon1 p4, p5, p6 against p11, p12, p13. That calculation will give us a shortest distance between p6 in polygon 1 and p13 in polygon2.

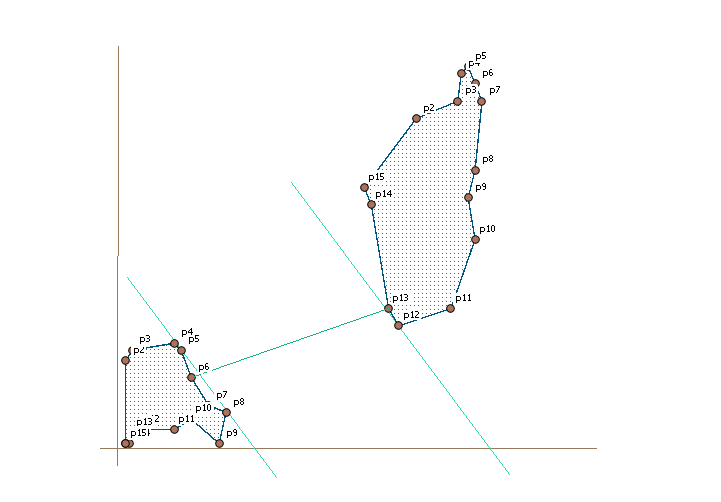
We now know that the distance we are searching is somewhere between the distance between the two parallel lines and the distance that we we have found between the points p6 and p13.

Now we take p5 from polygon1 and measure that to the points in polygon2 in order from closest to the line to more far away. We continue til we have reached the point that is that far from the left line like the shortest distance we have found that far. Then we take the next point in polygon1, p8 that is the point next closest to the line and do the same procedure, measuring against each point in polygon2 until we are «out of reach» for the already found shortest distance. This way we continue until the next point in polygon1 we are picking up is more far away from the right of the parallel lines than the shortest distance we have found. Then there can be no shorter distances to find. As mentioned earlier every check between two points include checking the point before and the point after including the edges in between.

The result is a distance calculated like described by this line from st_shortestline.